Complexe impedanties

Terug naar de index.

Met de volgende calculator worden diverse eigenschappen berekend van een seriekring bestaande uit een weerstand en een spoel of condensator.
Vul de frequentie, weerstand en spoel / condensator waarde in de geel gekleurde velden in, en klik op "bereken".

Hieronder wordt uitgelegd wat de calculator uitrekent.

Wat is impedantie

Impedantie is een soort weerstandwaarde welke een elektrisch component schijnt te hebben bij een bepaalde frequentie.
De impedantie geven we aan met de letter X, de eenheid is Ω (Ohm).
Voor een weerstand is de impedantie: X=R
Voor een spoel is de impedantie: X=2.pi.f.L
Voor een condensator is de impedantie: X= 1/(2.pi.f.C)

X = impedantie (Ω)
pi  =3,1415
f   =frequentie (Hertz)
L = inductie van de spoel (Henry)
C  = capaciteit van de condensator (Farad)

Deze manier van weergeven van de impedantie is echter niet volledig, omdat we de fase tussen spanning en stroom niet weergeven.
Aan de waarde van X kunnen we niet zien of we te doen hebben met een weerstand, spoel of condensator.
 

Complexe impedantie

Een complexe impedantie is opgebouwd uit een reëel deel (R = weerstand) in serie met een imaginair deel (+JX = spoel of -JX = condensator)
Een complexe impedantie geven we aan met de letter Z, en de eenheid is Ω.

De notatie voor complexe impedantie kan zijn Z=R+JX.
In dit geval staan een weerstand R en spoel in serie.
De impedantie van de spoel is: X=2.pi.f.L
Bij een spoel loopt (bij wisselstroom) de spanning altijd 90° voor op de stroom, dit geven we aan met +J.

De notatie voor complexe impedantie kan ook zijn: Z=R-JX.
In dit geval staan een weerstand en een condensator in serie.
De impedantie van de condensator is: X= 1/(2.pi.f.C)
Bij een condensator loopt (bij wisselstroom) de spanning altijd 90° achter op de stroom, dit geven we aan met de -J.
 

Voorbeeld 1:   Z1=220+J300 Ω.
In dit voorbeeld zijn een weerstand van 220 Ω en een spoel met een impedantie van 300 Ω in serie geschakeld.
Deze twee componenten in serie vormen één complexe impedantie.

Voorbeeld 2:  Z2=470-J80 Ω
In dit voorbeeld zijn een weerstand van 470 Ω en een condensator met een impedantie van 80 Ω in serie geschakeld.

Voorbeeld 3: Z3=100+J0 Ω  
Dit is een zuivere weerstand van 100 Ω (op die frequentie)
Omdat het imaginaire deel nul is, kun je ook schrijven Z3=100-J0 Ω

Voorbeeld 4: Z4= 0+J60 Ω
Dit is een spoel met een impedantie van 60 Ohm, deze spoel heeft geen serieweerstand.

Voorbeeld 5: Z5=0-J400 Ω
Dit is een condensator met een impedantie van 400 Ω, deze condensator heeft geen serieweerstand.

De J operator

De letter J in complexe impedanties noemen we de J operator.

Bij een weerstand zijn de spanning over de weerstand, en de stroom erdoor met elkaar in fase, er is geen faseverschil.
De impedantie van een weerstand noemen we een reële impedantie.

De impedantie van een spoel is niet reëel maar imaginair.
Bij een spoel loopt (bij wisselstroom) de spanning altijd 90° voor op de stroom, dit geven we aan met +J gevolgd door de impedantiewaarde.

Ook bij een condensator hebben we een imaginaire impedantie.
Bij een condensator loopt (bij wisselstroom) de spanning altijd 90° achter op de stroom, we geven dit aan met -J gevolgd door de impedantiewaarde.
 

Rekenen met de J operator

Als we gaan rekenen met imaginaire impedantie, gelden de volgende regels:

J = √-1

J² = -1

1/J = -J

1/-J = J

Ja + Jb = J(a+b)

J-a = -Ja

Het optellen van complexe impedanties

Als we twee complexe impedanties in serie schakelen ontstaat er een nieuwe complexe impedantie.
Bij het optellen kunnen we de reële delen bij elkaar optellen en ook de imaginaire delen kunnen we bij elkaar optellen.
Bijvoorbeeld: Z1 en Z2 schakelen we in serie, de som van deze twee is Z6

Z1=220+J300 Ω
Z2=470-J80    Ω    +
Z6=690+J220 Ω

De imaginaire delen tellen bij elkaar op, maar omdat bij Z2 het imaginaire deel negatief is, wordt het in wezen afgetrokken van het imaginaire deel van Z1.
 

Nog een voorbeeld: Z7=Z1+Z2+Z3+Z4+Z5

Z1=220+J300 Ω.
Z2=470-J80 Ω
Z3=100+J0 Ω
Z4=   0+J60 Ω
Z5=   0-J400 Ω   +
Z7=790-J120 Ω

De som van al deze impedanties gedraagt zich op die frequentie hetzelfde als een een weerstand van 790 Ω in serie met een condensator met 120 Ω impedantie.
 

Resonantie

Als we een condensator en spoel in serie zetten, en het imaginaire deel van beide is even groot, dat zullen deze opgeteld nul Ω zijn.
Dit circuit is dan in serieresonantie, we houden alleen de weerstand van beide componenten over.
In serieresonantie heeft de impedantie van een LC kring de laagste waarde.

Bij een parallel LC schakeling zal bij resonantie, de impedantie juist de hoogste waarde bereiken
 

De Q factor

Van een complexe impedantie kunnen we de kwaliteitsfactor (Q) uitrekenen.
De Q is de verhouding tussen het imaginaire deel en het reële deel van de impedantie.

Q=X/R
Het doet er niet toe of het imaginaire deel positief of negatief is, we nemen in de berekening alleen het getal achter de J.
De Q factor heeft geen eenheid, de waarde is altijd positief (of nul in het geval van een pure weerstand).

Voorbeeld: Z7=790-J120 Ω heeft een Q van 0,1519

De absolute waarde van de impedantie

Als we een wisselspanning aansluiten op de complexe impedantie dan zal er een stroom gaan lopen.
Om de waarde van deze stroom te kunnen berekenen hebben we de absolute waarde van de impedantie nodig.
De absolute waarde geven we aan met |Z| en heeft de eenheid Ω.

Voor een complexe impedantie Z=R±JX is de absolute waarde:
|Z| = √(R² + X²)

Voorbeeld Z7=790-J120 Ω
|Z7| = √(790² + 120²) =   799 Ω.

Als we deze impedantie aansluiten op een wisselspanning dan zal er een stroom gaan lopen met de waarde:
 I = U / |Z|
Voorbeeld: de spanning over Z7 is 10Volt RMS.
|Z7|= 799 Ohm
I=10 / 799 = 0,0125 Ampere RMS.
 

Faseverschil tussen spanning en stroom

De fase tussen de spanning over de complexe impedantie en de stroom erdoor kunnen we als volgt berekenen:

Fase = arctangens (±X/R).
De eenheid is graden ( ° )

De X waarde kan zowel positief zijn, als negatief, overeenkomstig het teken voor de J operator.
Een positieve waarde van de fase geeft aan dat de spanning voorloopt op de stroom.
Een negatieve waarde van de fase geeft aan dat de spanning achterloopt op de stroom.

De waarde van de fase kan variëren van  +90° (spoel), via 0° (weerstand) tot -90° (condensator).

Voorbeeld:
Bij een complexe impedantie van Z7=790-J120 Ω bedraagt de fase tussen spanning en stroom:
fase= arctangens (-120 / 790) = -8,6°
 

Impedanties als vectoren

Complexe impedanties kunnen we als vectoren (pijlen) in een diagram geplaatst worden.

De hoek met de horizontale as, geeft de fase weer tussen tussen spanning en stroom, de lengte van de vector komt overeen met de waarde van de impedantie.

Een complexe impedantie: Z8=4+J3 Ω De lengte van de vector Z8 is gelijk aan de absolute waarde |Z8|. In dit geval: |Z8|=√(4²+3²)= 5 Ω

Twee complexe impedanties (Z8 en Z9) zijn in serie geschakeld. Z10 is de som van Z8 en Z9, dus Z10=Z8+Z9

Omzetten van serie impedantie naar parallel impedantie

Een complexe impedantie bestaande uit de serieschakeling van een weerstand en een spoel / condensator kunnen we ook omrekenen naar een parallel schakeling van een weerstand met een spoel / condensator.
Beide schakelingen zullen zich op die frequentie volledig hetzelfde gedragen, maar dat geldt alleen op één frequentie waar we het circuit voor berekenen.

	Een serieschakeling van weerstand en spoel wordt omgezet naar een parallel schakeling van weerstand en spoel
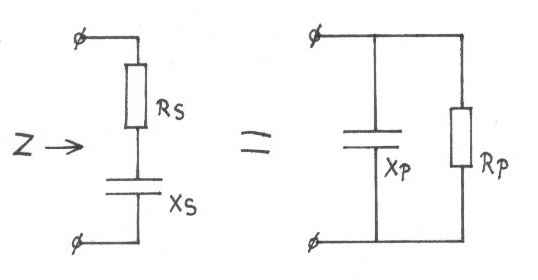	Een serie schakeling van weerstand en condensator wordt omgezet naar een parallel schakeling van weerstand en condensator

Het omzetten gaat als volgt,
We hebben een complexe serieschakeling Z=RS+JXS
RS en XS zijn de seriecomponenten.

Met de volgende formules vinden we de waarden van de parallel componenten RP en XP.
Rp = (RS²+XS²)/RS

Xp = J(RS²+XS²)/XS

Indien de complexe impedantie capacitief is, dus Z=RS-JXS dan krijgt de waarde van XP een negatieve waarde.
 

Voorbeeld1:
De complexe impedantie is Z=20+J15 Ω
De parallel impedanties zijn:
RP = (20²+15²)/20 = 31,25 Ω
XP = J(20²+15²)/15 = +J41,67 Ω
Een serieschakeling van weerstand en spoel wordt dus omgezet naar een parallelschakeling van weerstand en spoel

Voorbeeld2:
Dezelfde componentwaarden, maar nu voor een capacitieve impedantie
De complexe impedantie is Z=20-J15 Ω
De parallel impedanties zijn:
RP = (20²+(-15)²)/20 = 31,25 Ω
XP = J(20²+(-15)²)/-15 = -J41,67 Ω
Een serieschakeling van weerstand en condensator wordt dus omgezet naar een parallelschakeling van weerstand en condensator.

Terug naar de index.